Poincaré Universe
Extract from A.B. Sossinsky’s Geometries 7.8 Hyperbolic Geometry and the Physical World
In his famous book Science et Hypothèse, Henri Poincaré describes the physics of a small “universe” and the physical theories that its inhabitants would create. The universe considered by Poincaré is Euclidean, plane (two-dimensional), and has the form of an open unit disk. Its temperature is $100^{\circ}$ Farenheit at the center of the disk and decreases linearly to absolute zero at its boundary. The lengths of objects (including living creatures) are proportional to temperature.
How will a little flat creature endowed with reason and living in this disk describe the main physical laws of his universe? The first question he/she may ask could be: Is the world bounded or infinite? To answer this question, an expedition is organized; but as the expedition moves towards the boundary of the disk, the legs of the explorers become smaller, their steps shorter - they will never reach the boundary, and conclude that the world is infinite.
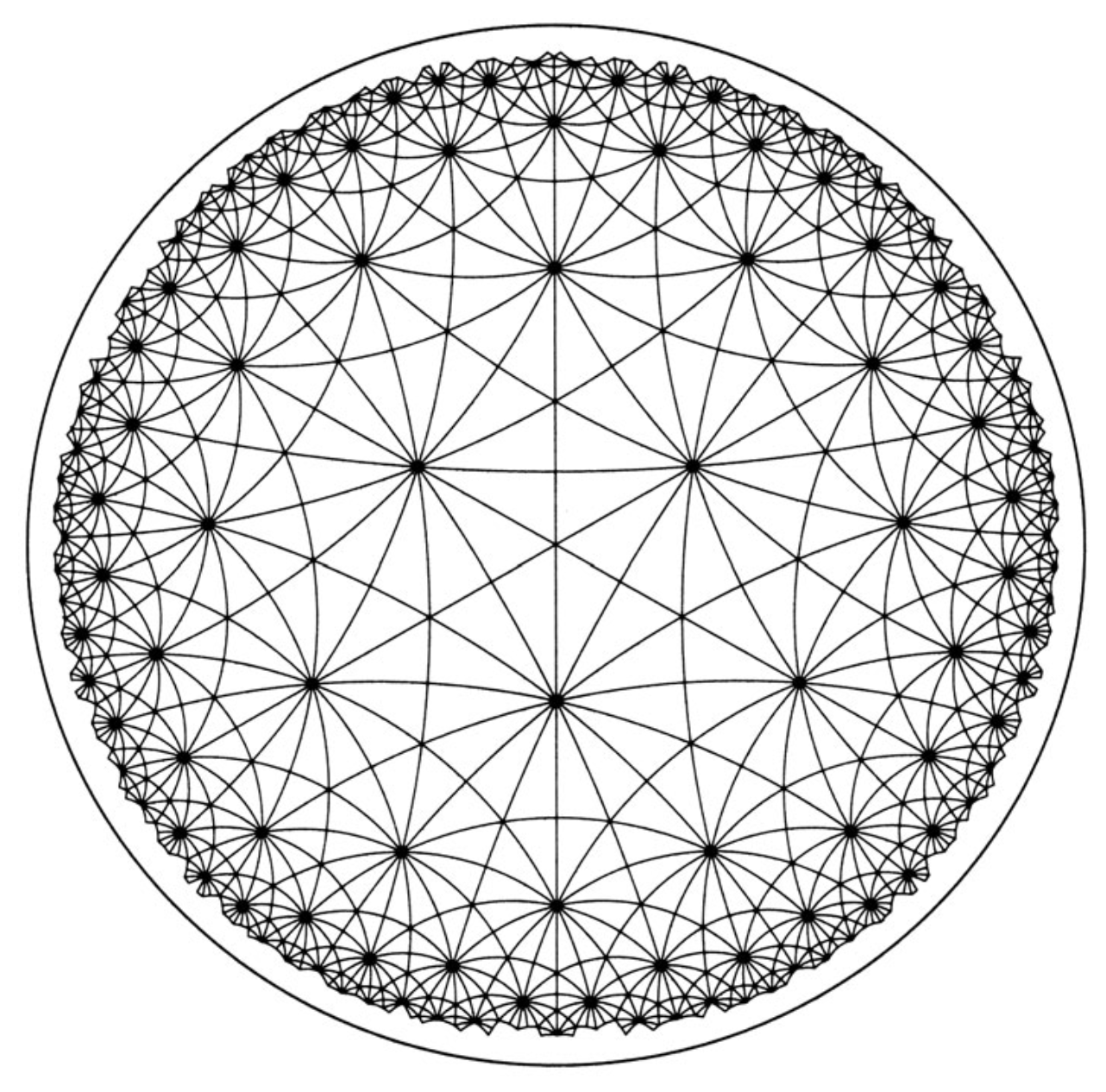
Figure 7.11 from Geometries
The next question may be: Does the temperature in the universe vary? Having constructed a thermometer (based on different expansion coefficients of various materials), scientists carry it around the universe and take measurements. However, since the lengths of all objects change similarly with temperature, the thermometer gives the same measurement all over the universe - the scientists conclude that the temperature is constant.
Then the scientists might study straight lines, i.e., investigate what is the shortest path between two points. They will discover that the shortest path is what we perceive to be the arc of the circle containing the two points and orthogonal to the boundary disk (this is because such a circular path brings the investigator nearer to the center of the disk, and thus increases the length of his steps). Further, they will find that the shortest path is unique and regard such paths as “straight lines”.
Continuing to develop geometry, the inhabitants of Poincaré’s little flat universe will decide that there is more than one parallel to a given line passing through a given point, the sum of angles of triangles is less than $\pi$, and obtain other statements of hyperbolic geometry.
Thus they will come to the conclusion that they live in an infinite flat universe with constant temperature governed by the laws of hyperbolic geometry. But this is not true - their universe is a finite disk, its temperature is variable (tends to zero towards the boundary) and the underlying geometry is Euclidean, not hyperbolic!
The philosophical conclusion of Poincaré’s argument is not agnosticism - he goes further. The physical model described above, according to Poincaré, shows not only that the truth about the universe cannot be discovered, but that it makes no sense to speak of any “truth” or approximation of truth in science - pragmatically, the inhabitants of his physical model are perfectly right to use hyperbolic geometry as the foundation of their physics because it is convenient, and it is counterproductive to search for any abstract Truth which has no practical meaning anyway.
This conclusion has been challenged by other thinkers, but we will not get involved in this philosophical discussion.