Covering Spaces of Wedge of Two Circles
We start with some theorems from Hatcher’s algebraic topology and will give a solution of the following exercise by enumeration.
- Find all the connected 2-sheeted and 3-sheeted covering spaces of $S^1 \vee S^1$, up to isomorphism of covering spaces without basepoints.
Review of Hatcher
Proposition 1.32. The number of sheets of a covering space $p:(\widetilde{X}, \widetilde{x_0}) \to (X, x_0)$ with $X$ and $\widetilde{X}$ path-connected equals the index of $p_*\left(\pi_1\left(\widetilde{X}, \widetilde{x_0}\right)\right)$ in $\pi_1\left(X, x_0\right)$.
*Proof*: For a loop $g$ in $X$ based at $x_0$, let $\widetilde{g}$ be its lift to $\widetilde{X}$ starting at $\widetilde{x_0}$. A product $h \cdot g$ with $[h] \in H=p_*\left(\pi_1\left(\widetilde{X}, \widetilde{x_0}\right)\right)$ has the lift $\widetilde{h} \cdot \widetilde{g}$ ending at the same point as $\widetilde{g}$ since $\widetilde{h}$ is a loop. Thus we may define a function $\Phi$ from cosets $H[g]$ to $p^{-1}\left(x_0\right)$ by sending $H[g]$ to $\widetilde{g}(1)$. The path-connectedness of $\widetilde{X}$ implies that $\Phi$ is surjective since $\widetilde{x_0}$ can be joined to any point in $p^{-1}\left(x_0\right)$ by a path $\widetilde{g}$ projecting to a loop $g$ at $x_0$. To see that $\Phi$ is injective, observe that $\Phi\left(H\left[g_1\right]\right)=\Phi\left(H\left[g_2\right]\right)$ implies that $g_1 \cdot \bar{g}_2$ lifts to a loop in $\widetilde{X}$ based at $\widetilde{x_0}$, so $\left[g_1\right]\left[g_2\right]^{-1} \in H$ and hence $H\left[g_1\right]=H\left[g_2\right]$. $\square$
Proposition 1.36. Suppose $X$ is path-connected, locally path-connected, and semilocally simply-connected. Then for every subgroup $H \subset \pi_1\left(X, x_0\right)$ there is a covering space $p: X_H \to X$ such that $p_*\left(\pi_1\left(X_H, \widetilde{x_0}\right)\right)=H$ for a suitably chosen basepoint $\widetilde{x_0} \in X_H$.
Proof: For points $[\gamma],\left[\gamma^{\prime}\right]$ in the simply-connected covering space $\widetilde{X}$ constructed above, define $[\gamma] \sim\left[\gamma^{\prime}\right]$ to mean $\gamma(1)=\gamma^{\prime}(1)$ and $\left[\gamma \cdot \overline{\gamma^{\prime}}\right] \in H$. It is easy to see that this is an equivalence relation since $H$ is a subgroup: it is reflexive since $H$ contains the identity element, symmetric since $H$ is closed under inverses, and transitive since $H$ is closed under multiplication. Let $X_H$ be the quotient space of $\widetilde{X}$ obtained by identifying $[\gamma]$ with $\left[\gamma^{\prime}\right]$ if $[\gamma] \sim\left[\gamma^{\prime}\right]$. Note that if $\gamma(1)=\gamma^{\prime}(1)$, then $[\gamma] \sim\left[\gamma^{\prime}\right]$ iff $[\gamma \cdot \eta] \sim\left[\gamma^{\prime} \cdot \eta\right]$. This means that if any two points in basic neighborhoods $U_{[\gamma]}$ and $U_{\left[y^{\prime}\right]}$ are identified in $X_H$ then the whole neighborhoods are identified. Hence the natural projection $X_H \to X$ induced by $[\gamma] \mapsto \gamma(1)$ is a covering space.
If we choose for the basepoint $\widetilde{x_0} \in X_H$ the equivalence class of the constant path $c$ at $x_0$, then the image of $p_*: \pi_1\left(X_H, \widetilde{x_0}\right) \to \pi_1\left(X, x_0\right)$ is exactly $H$. This is because for a loop $\gamma$ in $X$ based at $x_0$, its lift to $\widetilde{X}$ starting at [c] ends at $[\gamma]$, so the image of this lifted path in $X_H$ is a loop iff $[\gamma] \sim[c]$, or equivalently, $[\gamma] \in H$. $\square$
Theorem 1.38 (Classification Theorem). Let $X$ be path-connected, locally path-connected, and semilocally simply-connected. Then there is a bijection between the set of basepoint-preserving isomorphism classes of path-connected covering spaces $p:\left(\widetilde{X}, \widetilde{x_0}\right) \to\left(X, x_0\right)$ and the set of subgroups of $\pi_1\left(X, x_0\right)$, obtained by associating the subgroup $p_*\left(\pi_1\left(\widetilde{X}, \widetilde{x_0}\right)\right)$ to the covering space $\left(\widetilde{X}, \widetilde{x_0}\right)$. If basepoints are ignored, this correspondence gives a bijection between isomorphism classes of path-connected covering spaces $p: \widetilde{X} \to X$ and conjugacy classes of subgroups of $\pi_1\left(X, x_0\right)$. $\square$
Proposition 1.39 (a) Let $p:\left(\widetilde{X}, \widetilde{x_0}\right) \to\left(X, x_0\right)$ be a path-connected covering space of the path-connected, locally path-connected space $X$, and let $H$ be the subgroup $p_*\left(\pi_1\left(\widetilde{X}, \widetilde{x_0}\right)\right) \subset \pi_1\left(X, x_0\right)$. Then this covering space is normal iff $H$ is a normal subgroup of $\pi_1\left(X, x_0\right)$. $\square$
proof: We observed earlier in the proof of the classification theorem (Theorem 1.38) that changing the basepoint $\widetilde{x_0} \in p^{-1}\left(x_0\right)$ to $\widetilde{x_1} \in p^{-1}\left(x_0\right)$ corresponds precisely to conjugating $H$ by an element $[\gamma] \in \pi_1\left(X, x_0\right)$ where $\gamma$ lifts to a path $\widetilde{\gamma}$ from $\widetilde{x_0}$ to $\widetilde{x_1}$. Thus $[\gamma]$ is in the normalizer $N(H)$ iff $p_{*}\left(\pi_1(\widetilde{X}, \widetilde{x_0})\right)=p_*\left(\pi_1(\widetilde{X}, \widetilde{x_1})\right)$, which by the lifting criterion is equivalent to the existence of a deck transformation taking $\widetilde{x_0}$ to $\widetilde{x_1}$. Hence the covering space is normal iff $N(H)=\pi_1\left(X, x_0\right)$, that is, iff $H$ is a normal subgroup of $\pi_1\left(X, x_0\right)$. $\square$
Problem solution
Problem:
find all the connected 2-sheeted and 3-sheeted covering spaces of $S^1 \vee S^1$, up to isomorphism of covering spaces without basepoints.
soln:
First note that $X=S^1 \vee S^1$ is path connected and locally path-connected and the latter property is also inherited by the covering space $\widetilde{X}$, so $\widetilde{X}$ is connected iff path-connected. By proposition 1.32 we see each 2 -sheeted cover $p: \widetilde{X} \to X$ has its induced subgroup $H=$ $p_*\left(\pi_1(\widetilde{X})\right)$ with index 2 in $\pi_1(X)=\pi_1\left(S^1 \vee S^1\right)=\langle a\rangle *\langle b\rangle$. Thus, by classification theorem (Theorem 1.38), we see classifying connected 2 -sheeted covering spaces up to isomorphism is equivalently of finding all index-2 subgroups of $F_2=\langle a\rangle *\langle b\rangle$. It can be shown that every index-2 subgroup is normal (by using the fact that the complement is a coset), so the 2-element group $F_2 / H$ is cyclic of order 2, i.e., isomorphic to $\mathbb{Z}_2$. By counting on the ways that $f:F_2 \to F_2 / H \cong \mathbb{Z}_2$ sends generators $a, b$ to $[0]$, $[1]$ we can classify these subgroups.
Since the canonical projection $f$ is surjective we see we only have three possible compositions: (1) $a \mapsto[0], b \mapsto[1]$, (2) $a \mapsto[1], b \mapsto[0]$, (3) $a \mapsto[1], b \mapsto[1]$. For (1) we see $a$ is send to identity so $a$ should be in the quotient, $b$ is send to the element in $\mathbb{Z}_2$ whose square is identity so $b^2$ should be in the quotient, and element $a b a^{-1}$ is added to make it the quotient indeed a normal subgroup, i.e., it is added to make $H$ a normal closure of $\set{a, b^2}$. Thus, (1) corresponds to $H_1=\left\langle b, a^2, a b a^{-1}\right\rangle$. Similarly, $H_2=\left\langle a, b^2, b a b^{-1}\right\rangle$ and $H_3=\left\langle a^2, b^2, a b\right\rangle$.
Since each $H_i$ is normal in $F_2$, each of them forms a single conjugacy class. Then use proposition 1.36 to find corresponded covering space $X_{H_i}$ (the process of finding $X_{H_i}$ in 1.36 is constructive), which are graphically represented by Hatcher in table on page 58 (below) ((1) and (2) in the table with another one switching $a$ and $b$ in (1))
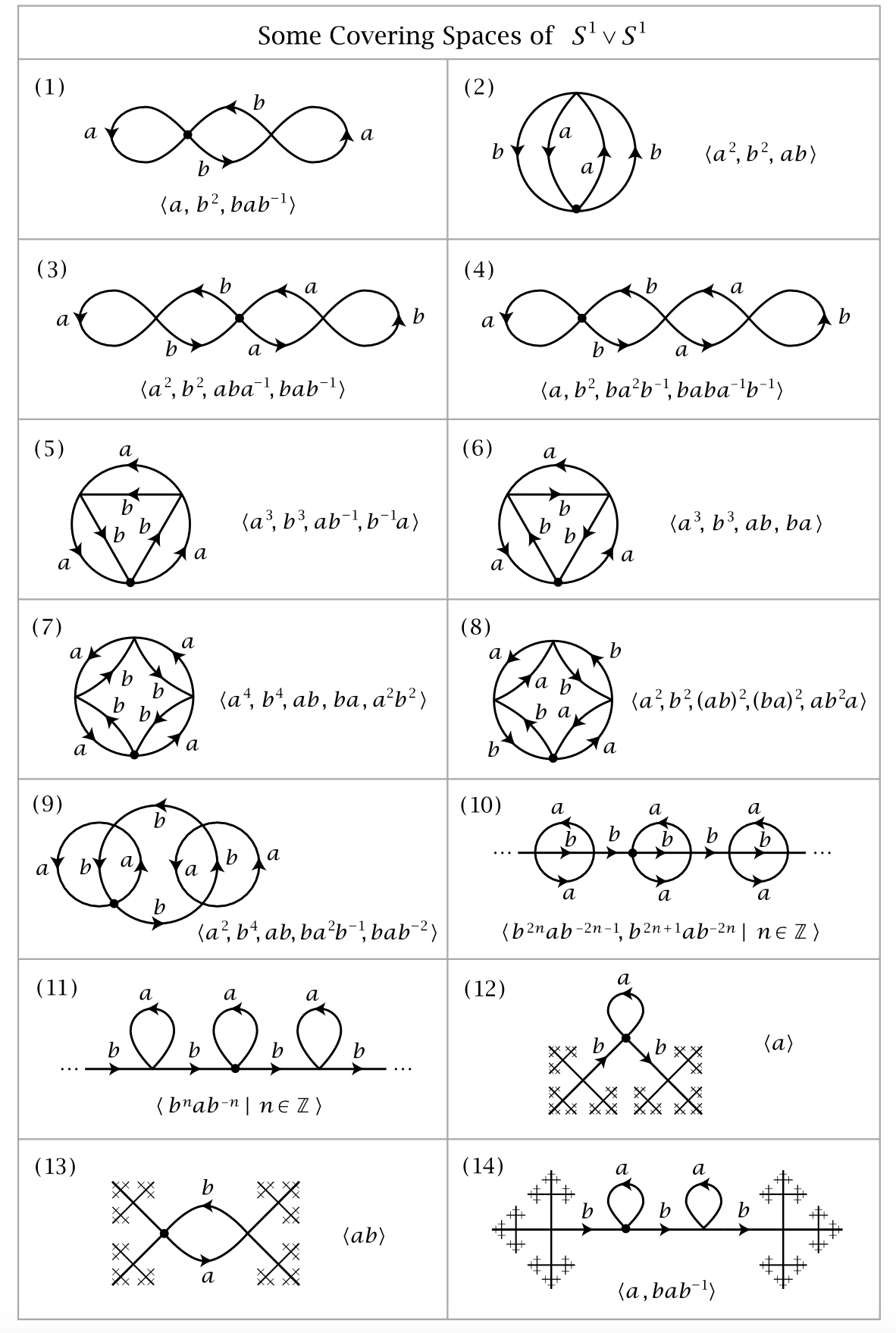
Some Covering Spaces of Wedge of Two Circles (Hatcher p.58)
Remark: We set the vertex of $S^1 \vee S^1$ as $x$ and two vertices $y_1, y_2 \in p^{-1}(x)$. Then $p_*\left(\pi_1\left(X_{H_1}, y_1\right)\right)=p_*\left(\pi_1\left(X_{H_1}, y_2\right)\right)$, as one can check that changing base point from left vertex $y_1$ of the above graph $X_{H_1}$ to vertex $y_2$ on the right still get three generating loops $b, a, a b a^{-1}$. This is simply a consequence of the symmetry of $X_{H_1}$. Therefore, the claim in Lee 11.34 is not violated. As Hatcher claims on page 71, $X_{H_2}$ and $X_{H_3}$, the graphs (1) and (2) on his original table, are normal covers, which happens by proposition 1.39 (a) if and only if the induced subgroup is normal in $\pi_1(X)=F_2$. And this is the same for $X_{H_1}$. $\square$
Apart from this algebraic approach, one may also use the approach by action on fiber, which is much simpler and will be used for the next classification. This is detailed explained by Hatcher in page 68-70: $n$-sheeted covering spaces of $X$ are classified by equivalence classes of homomorphisms $\pi_1(X) \to S_n$. Therefore, we check all possible ways of mapping the generators $a$ and $b$ of $\pi_1(X)=F_2=\langle a\rangle *\langle b\rangle$ to elements in symmetric group $S_3$ an classify them. We have the following table of all $6 \times 6=36$ possible combinations:

3-sheeted Covering of $S^1\vee S^1$
each row is a possible way of sending $a$ to an element in $S_3=\set{(1),(1;2),(1;3),\left(2; 3\right),\left(1; 2;3\right),\left(1;3\right)}$, and each column is a possible way of sending $b$ to an element in $S_3$. We denote the covering space, the 2 -oriented graph, on $i$-th row and $j$ th column as $K(i, j)$. We use the notation on Hatcher page 69: for vertex $x_0$ in the wedge of two circle, we use $L_\gamma: p^{-1}\left(x_0\right) \to p^{-1}\left(x_0\right) ; \widetilde{\gamma}(0) \mapsto \widetilde{\gamma}(1)$ to denote one permutation on fiber $p^{-1}\left(x_0\right)$, where $\widetilde{\gamma}$ is the unique lift of the loop $\gamma$ with given starting point $\widetilde{\gamma}(0)$. Then $\gamma \mapsto$ $L_\gamma$ gives a homomorphism $\phi$ from $\pi_1\left(X, x_0\right)$ to the group of permutation of $p^{-1}\left(x_0\right)$ which is the same as $S_3$. Then we use $K(1,2)$ and $K(6,1)$ to exemplify how we obtain each graph $K(i, j)$ by example on $K(1,2)$. $K(1,2)$ : this is corresponded to $\phi(a)=(1), \phi(b)=(1;2)$. The loop $a$ in $X$ is sent to permutation $L_a=(1)=i d_{p^{-1}\left(x_0\right)}$, the identity on $\set{y_1, y_2, y_3}=p^{-1}\left(x_0\right)$, i.e., each lift is a loop with same starting and ending point. We labeled vertices $y_{1,2,3}$ as 1,2,3 on graph $K(1,2)$. The black edges with orientations show the associated lifts of $a$. Similarly, the red edges with orientations show the associated lifts of $b$, as $L_b=(12)$ means the lift $\widetilde{b}$ starting with $y_1$ ends at $y_2$; the lift $\widetilde{b}$ starting with $y_2$ ends at $y_1$; and the lift $\widetilde{b}$ starting with $y_3$ ends at $y_3$. In all, $(1)$ means identity on the fiber, $(1;2), (1;3), (2;3)$ give transposition on the fiber, and $\left(1; 2; 3\right), \left(1; 3; 2\right)$ give cyclic permutation. We then obtain the table above. We see that there are 10 of them disconnected: $$ K(1,1), K(1,2), K(1,3), K(1,4), K(2,1), K(2,3), K(3,1), K(3,3), K(4,1), K(4,4) $$
We then analyze the remaining $26$ covering spaces.
First see that $K(4,3)$ has the same induced subgroup as $K(3,4)$ : By choosing the basepoint at $y_3$ we directly read off all generating loops of $K(4,3)$ to obtain $$ \left\langle a^2, b^2, a b a^{-1}, b a b^{-1}\right\rangle $$
With the same basepoint at $y_3$ we directly read off all generating loops of $K(3,4)$ to obtain $$ \left\langle b^2, a^2, b a b^{-1}, a b a^{-1}\right\rangle $$
Therefore, their induced subgroups are the same, denoted as $H_{3443}$ and the two covers are put into the same basepoint-preserving isomorphism class of coverings (see classification theorem 1.38). $H_{3443}$ is also the case illustrated on (3) of the table in Hatcher page 58. $K(3,2)$ and $K(4,2)$ have the same induced subgroups $$ H_{234}=\left\langle a, b^2, b a^2 b^{-1}, b a b a^{-1} b^{-1}\right\rangle $$ by choosing basepoint $y_3 . H_{234}$ is also the case illustrated on (4) of the table in Hatcher page 58. $K(2,3)$ and $K(2,4)$ are put into the same basepoint-preserving isomorphism class of coverings. Now observe that $H_{3443}, H_{342}, H_{234}$ are all conjugate to each other because these covering spaces $\widetilde{X}$ only differ by basepoints $y_1, y_2, y_3$ (see second part of classification theorem 1.38). We denote this conjugacy class by $C_1$.
We by similar argument list the tuples (two graphs in the same iso class, basepoint $y_3$, induced subgp, conjugacy class) $$ \begin{aligned} & \left(K(5,1), K(6,1), y_3, H_{561}=\left\langle b, a^3, a b a^{-1}, a^{-1} b a\right\rangle, C_2\right) \newline & \left(K(5,2), K(6,2), y_3, H_{562}=\left\langle b, a^3, a b^2 a^{-1}\right\rangle, C_3\right) \newline & \left(K(5,3), K(6,4), y_3, H_{563}=\left\langle b^2, a^3, a b a^{-1}\right\rangle, C_3\right) \newline & \left(K(5,4), K(6,3), y_3, H_{564}=\left\langle b^2, a^3, a^{-1} b a\right\rangle, C_3\right) \newline & \left(K(1,5), K(1,6), y_3, H_{156}=\left\langle a, b^3, b a b^{-1}, b^{-1} a b\right\rangle, C_4\right) \newline & \left(K(2,5), K(2,6), y_3, H_{256}=\left\langle a, b^3, b a^2 b^{-1}\right\rangle, C_5\right) \newline & \left(K(3,5), K(4,6), y_3, H_{356}=\left\langle a^2, b^3, b a b^{-1}\right\rangle, C_5\right) \newline & \left(K(4,5), K(3,6), y_3, H_{456}=\left\langle a^2, b^3, b^{-1} a b\right\rangle, C_5\right) \end{aligned} $$
$\left(K(5,5), K(6,6), y_3, H_{5656}=\left\langle a^3, b^3, a b^{-1}, b^{-1} a\right\rangle, C_6\right)$ (also Hatcher p58, (5) of the able; also normal by Hatcher p71) $\left(K(5,6), K(6,5), y_3, H_{5665}=\left\langle a^3, b^3, a b, b a\right\rangle, C_7\right)$ (also Hatcher p58, (6) of the able; also normal by Hatcher p71)
There are in total 13 distinct subgroups of $\pi_1(X)$, corresponded to 13 isomorphism classes if we insist upon preservation of basepoint at $y_3$. They are $$ H_{3443}, H_{342}, H_{234}, H_{561}, H_{562}, H_{563}, H_{564}, H_{156}, H_{256}, H_{356}, H_{456}, H_{5656}, H_{5665} $$
To see there are no more than 13 subgroups we invoke a formula of computing the number $N(k, r)$ of index-k subgroups of rank-r free group: $$ N(k, r)=k(k !)^{r-1}-\sum_{i=1}^{k-1}((k-i) !)^{r-1} N(i, r) $$ The formula is form link. In particular $N(1,2)=1$ since the index-1 subgroup is just the whole group and $N(2,2)=3$ as we see from the first part of the problem and $$ \begin{aligned} N(3,2) & =3(3 !)^{2-1}-\sum_{i=1}^{3-1}((3-i) !)^{2-1} N(i, 2) \newline & =3 \cdot 6-2 \cdot N(1,2)-N(2,2) \newline & =18-2 \cdot 1-3=13 \end{aligned} $$
If we relax on the basepoint preservation condition, we have 7 isomorphism classes of connected covers with corresponded 7 conjugacy classes: $$ C_1, C_2, C_3, C_4, C_5, C_6, C_7 $$
Pictures of the representatives of these iso classes are shown in the table we gave.