Courses
This is a collection of lecture notes, assignments, links, and some other related materials of the courses I have taken.
1. Algebra
Thanks to Albert Peng for his permission to edit his tex file of Math5031 and also J.S. Milne’s tex file.
Math5031-32 Lecture Note, with homework incorporated as solved exercises
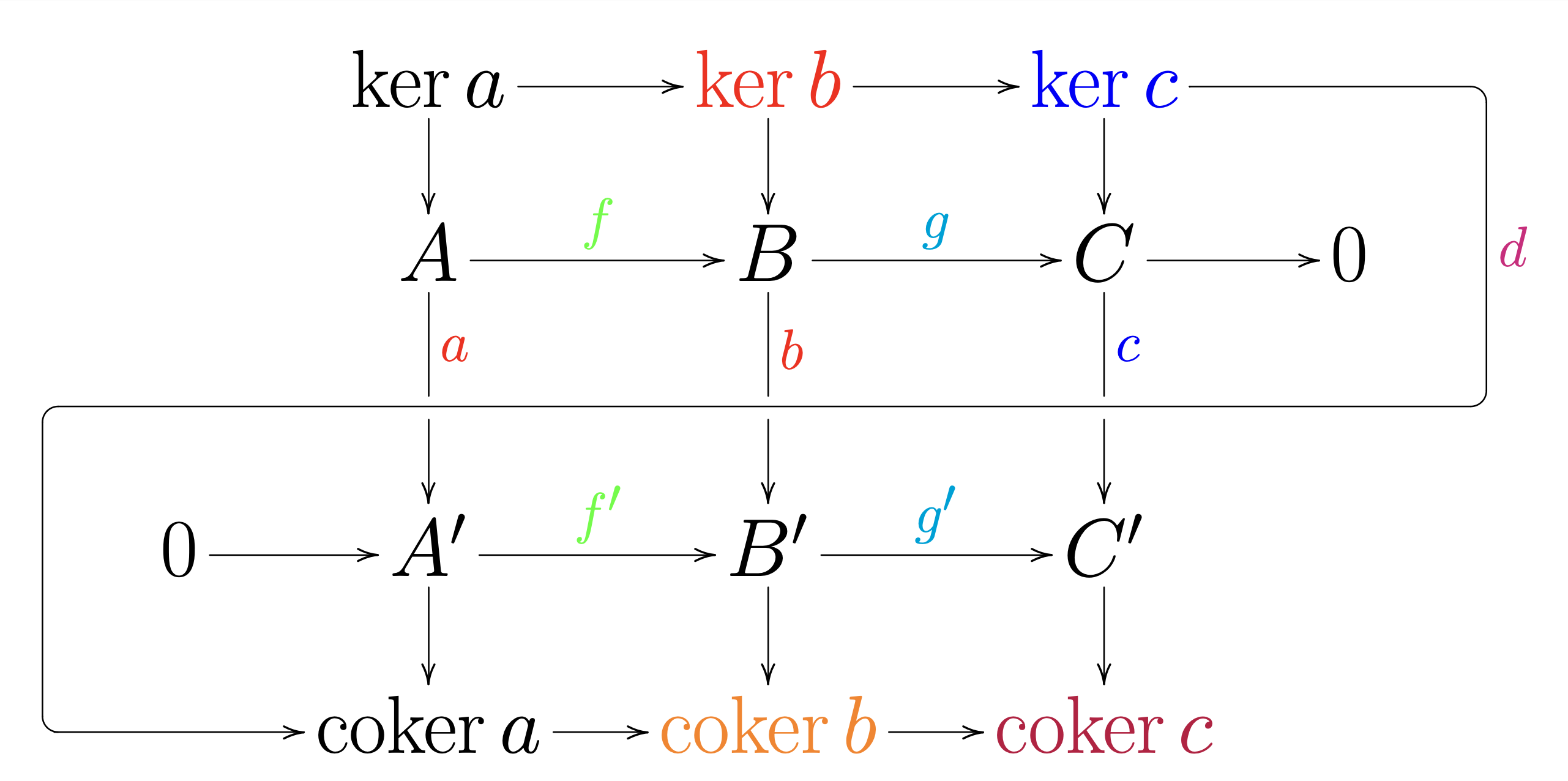
snake lemma. I add some colors to the code in https://commons.wikimedia.org/wiki/File:Snake_lemma_complete.svg
2. Algebraic Geometry
We use Algebraic Geometry by Robin Hartshorne as textbook but not follow it closely for some parts of the course. There will be homework on most weeks, and some of them will be chosen from Hartshorne. Some resources:
The red book of Varieties and Schemes, David Mumford. Springer Lecture Notes, 1999.
Lecture note by Andreas Gathmann.
3. Lie Algbera and Representation Theory
We used the following textbooks:
Introduction to Lie Algebras, by K. Erdmann and M. J. Wildon
Introduction to Lie Algebras and Representation Theory, by J. Humphreys
Representation Theory: A First Course, by W. Fulton and J. Harris
Symmetry, Representations, and Invariants, by R. Goodman and N. R. Wallach
Math547 Lecture Note
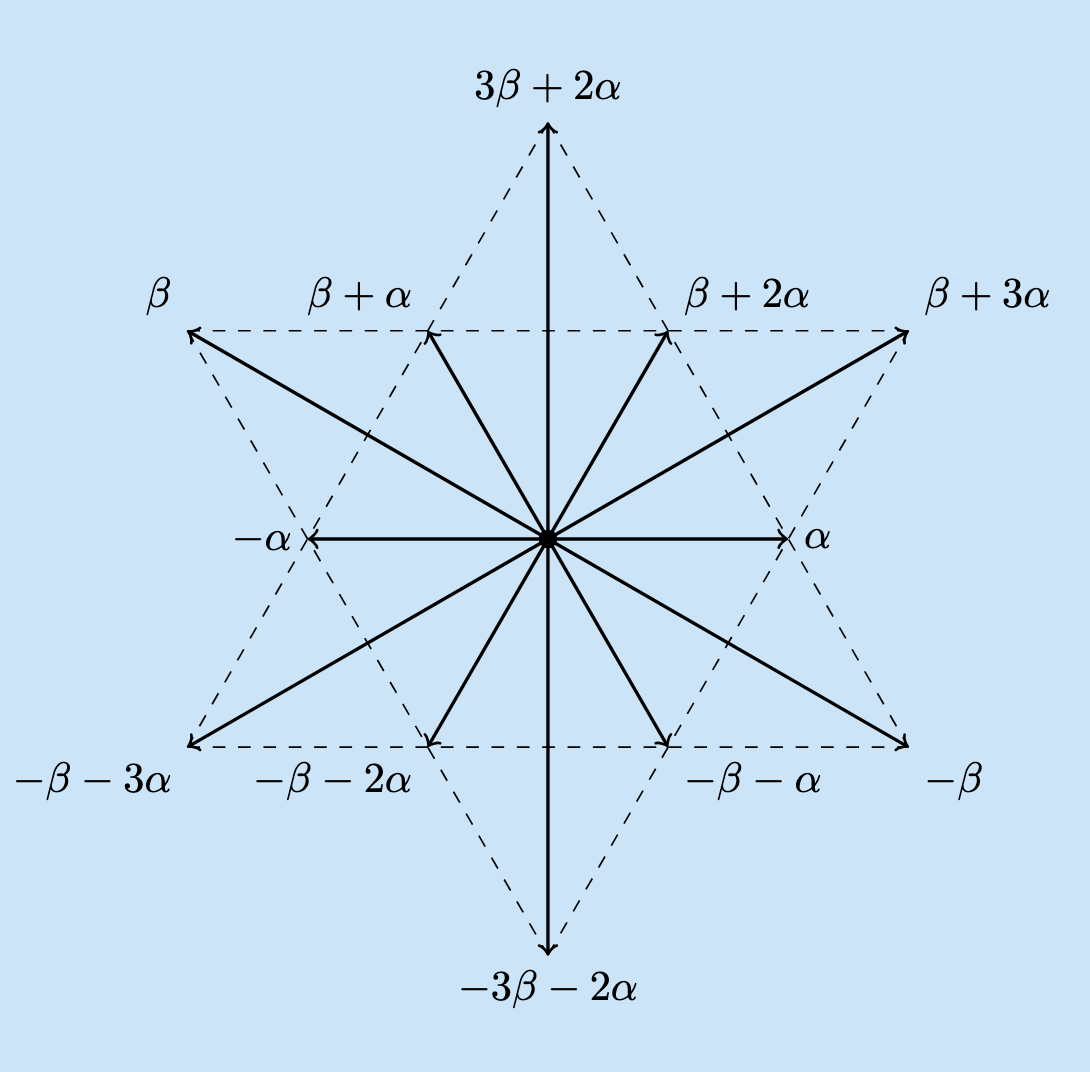
Root System G_2
4. Measure Theory and Functional Analysis
Math5051-52 Lecture Note
5. Complex Analysis
I transcribed Prof. Martinkainen’s written manuscripts into latex file, with several tikz illustrations.
I also add some useful remarks made by Prof. Steven Krantz in undergraduate complex analysis course Math416.
Math5021-22 Lecture Note
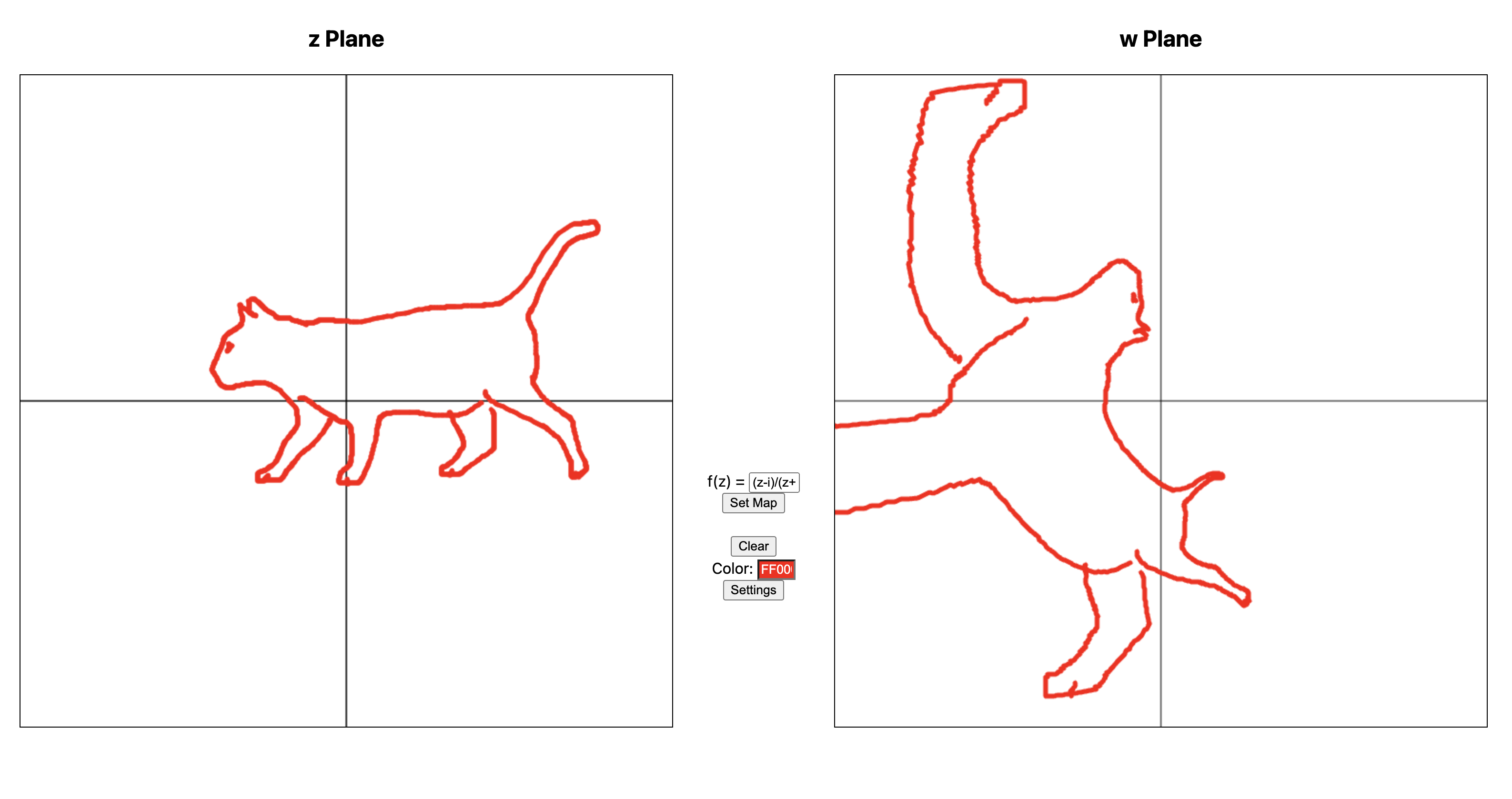
Cayley map
Above is the image of a cat by Cayley map $\frac{z-i}{z+i}$ visualized through online conformal mapping viewer. Cute cat becomes a bear.
6. Differential Equations
ODE: ODE lecture note, Lebl’s online tex file, Teschl’s Ordinary Differential Equations and Dynamical Systems.
Dynamical system and Chaos: Strogatz’s Nonlinear Dynamics and Chaos With Applications to Physics, Biology, Chemistry, and Engineering.
PDE: Evans’s Partial Differential Equations.
 pianist Emaneul Ax's signature on Lee's Intro to SM
pianist Emaneul Ax's signature on Lee's Intro to SM7. Differential Topology
We used John M. Lee’s Introduction to Smooth Manifold (e2) and Tu’s Introduction to Manifold (e2). Some other texts are also very interesting, including a classical little book Milnor’s Topology from the Differentiable Viewpoint and Smooth Manifolds and Observables by a group named themselves Jet Nestruev.
Lecture Note and Homework soln
8. Differential Geometry
We used John Lee’s Introduction to Riemannian Manifolds, Do Carmo’s Riemannian Geometry and other texts.
Math5047 Lecture Note
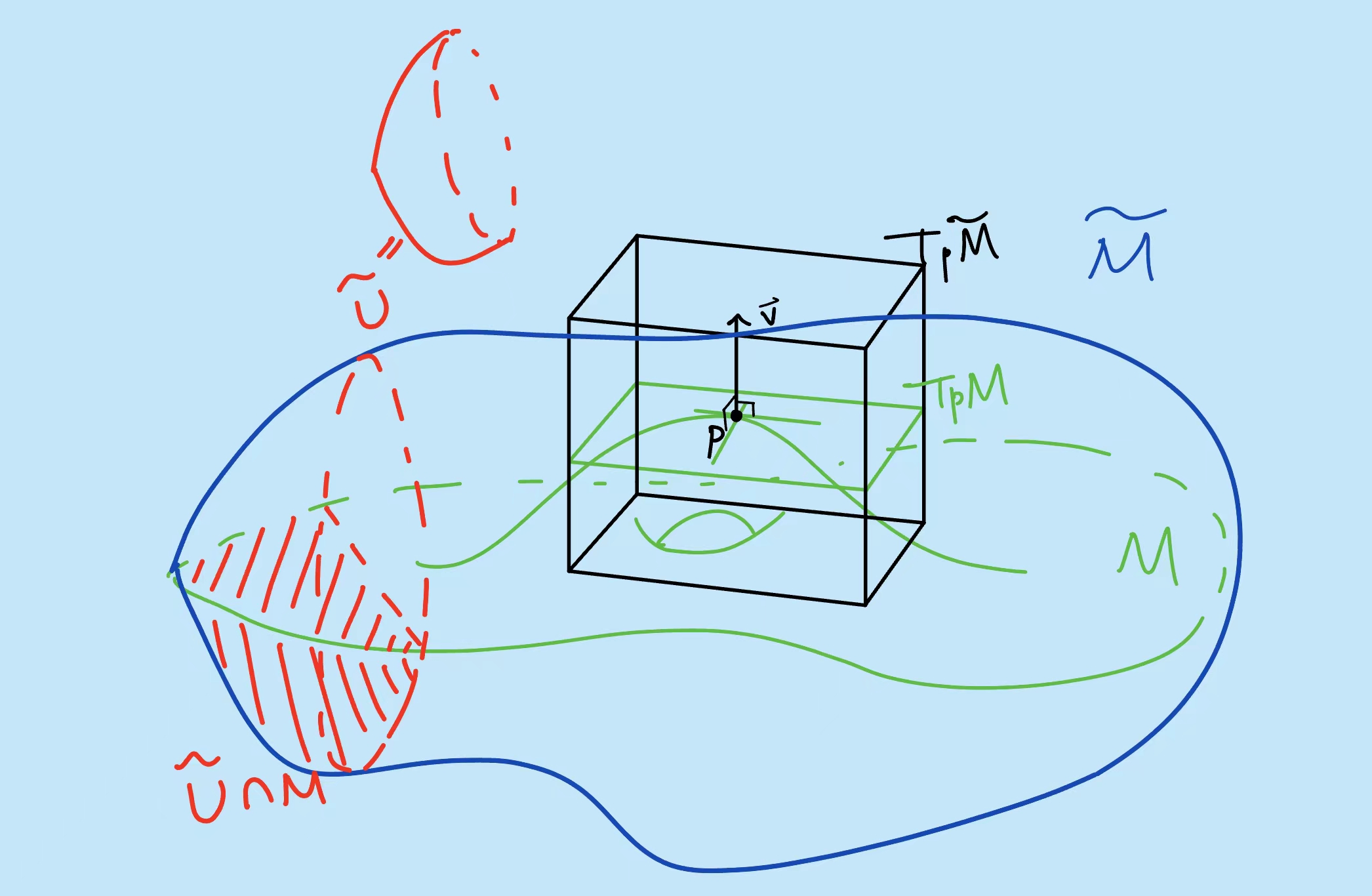
A Submanifold.
Undergraduate Course Projects
Network statistics lecture note and final presentaton on cross-validation
Computational geometry course slides, homework solns, and final project and demo
Group theory presentation: An Exposition of Modernism in Geometry and Physics
Split Spoils: Solution to Stolen Necklace Problem Via Borsuk-Ulam Theorem
More Pictures
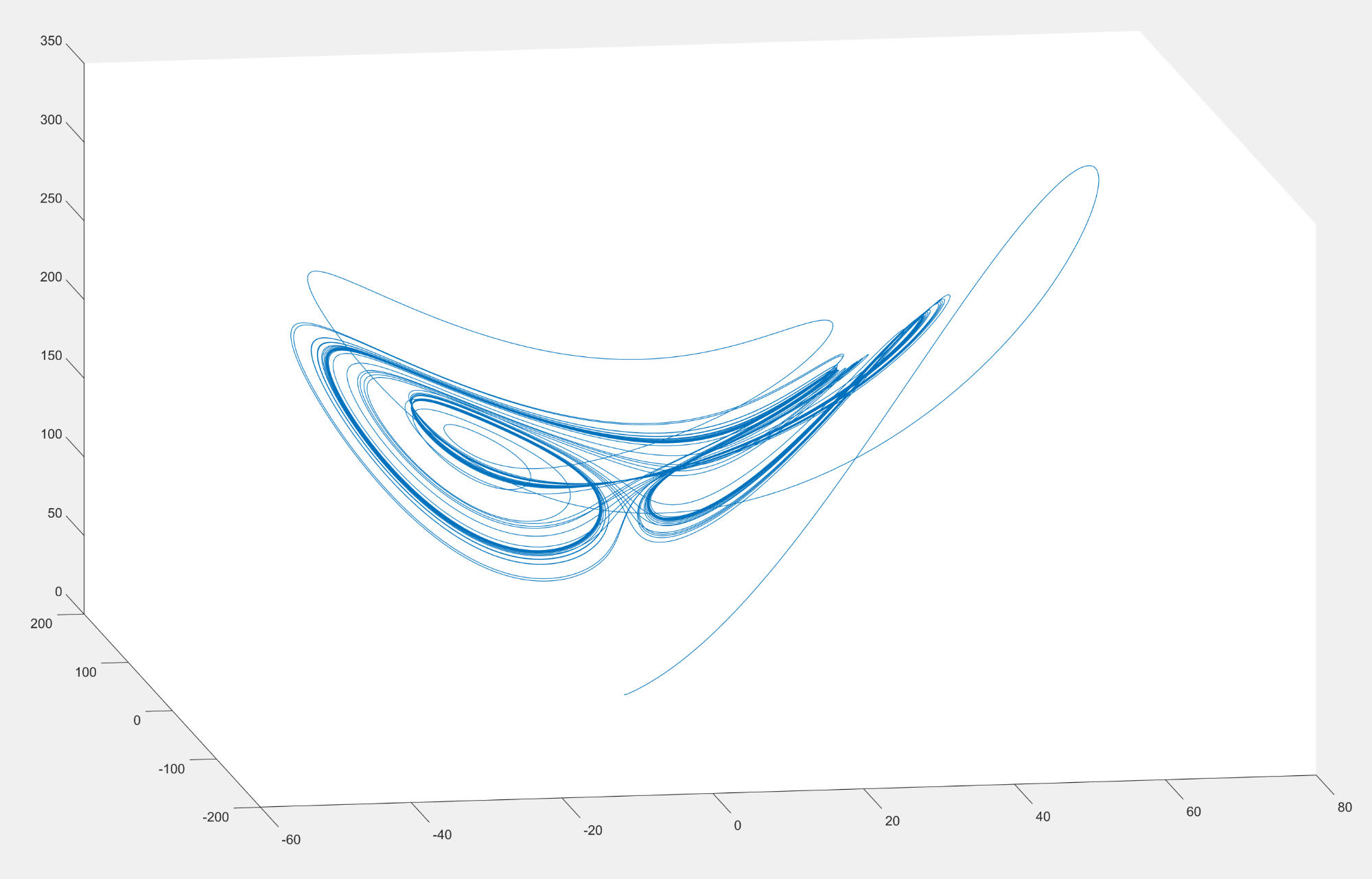
Lorenz system using Matlab
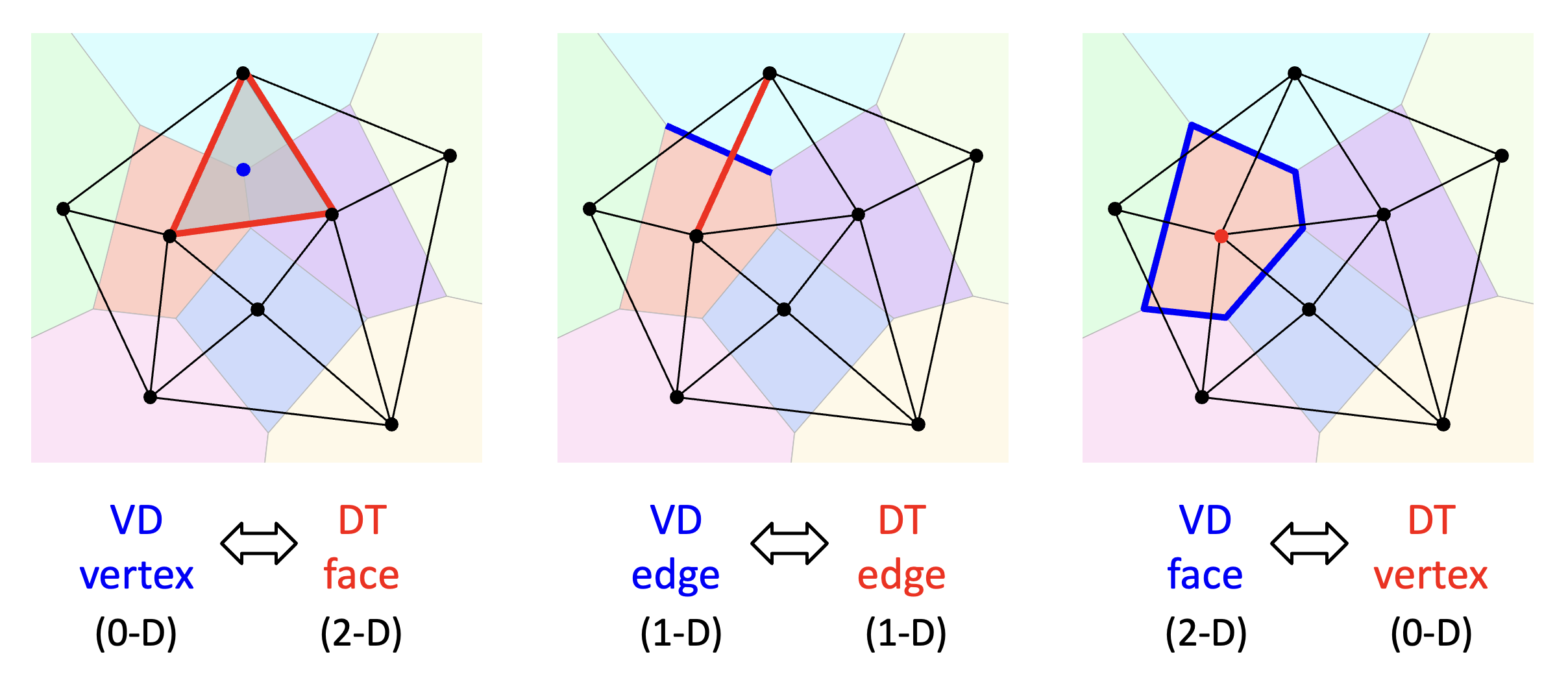
Voronoi Diagram - Delaunay Triangulation duality (Lecture 12 slide 27)