Asymptotes of algebraic curves
An asymptote of a curve is a straight line that the curve approaches as the points on the curve tend toward infinity. Essentially, the distance between the curve and the line becomes arbitrarily small as you move further along the curve. There are three main types of asymptotes:
- Vertical Asymptotes
- Horizontal Asymptotes
- Oblique Asymptotes
The Algebraic Method
Step 1: Replace $ y $ with $ mx + c $ (for $x \to \infty$ case)
Given the equation of the curve, replace $ y $ with the expression $ mx + c $. This transforms the equation into a polynomial form:
$$ a_n x^n + a_{n-1} x^{n-1} + \ldots + a_1 x + a_0 = 0 $$
Step 2: Solve the Simultaneous Equations
Next, solve the following system of equations for $ m $ and $ c $:
$$ a_n = 0 $$ $$ a_{n-1} = 0 $$
Step 3: Write the Equation of the Asymptote
For each pair of solutions $ m $ and $ c $, write the equation of the asymptote in the form:
$$ y = mx + c $$
Step 4: Handle Special Cases
If there is no $ a_{n-1} $ term in the polynomial (from Step 1), you should instead solve the system:
$$ a_n = 0 $$ $$ a_{n-2} = 0 $$
This step helps in finding the appropriate asymptote in cases where the usual process doesn’t directly apply.
Step 5: Consider the Case $ y \to \infty $
In addition to the $x \to \infty$ case, you should also consider the possibility of $ y \to \infty $. To do this, swap the roles of $ x $ and $ y $ in the equation. Replace $ x $ with $ ky + b $, which transforms the equation into:
$$ b_m y^m + b_{m-1} y^{m-1} + \ldots + b_1 y + b_0 = 0 $$
Then, repeat the process of solving the system of equations for $ k $ and $ b $:
$$ b_m = 0 $$ $$ b_{m-1} = 0 $$
The solutions give you the equations of any additional asymptotes, in the form:
$$ x = ky + b $$
Example
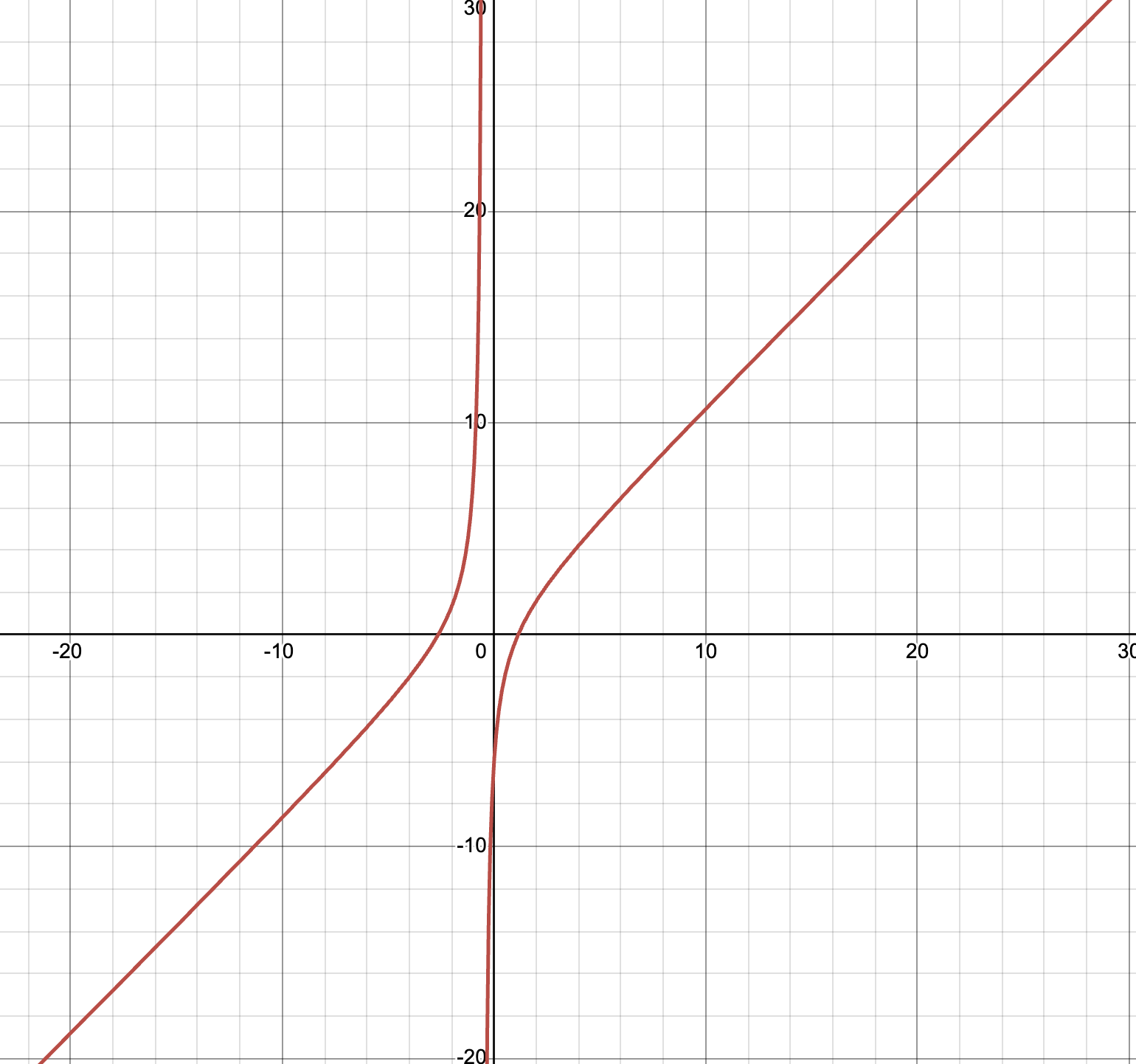
Find the asymptotes for $$ 2x^2+3x-2xy-y=6 $$
Let $y=mx+c$. We will get $$ (2-2m)x^2 + (3-m-2c)x - c -6=0 $$ Then we have $2-2m=0\implies m=1$ and $3-m-2c=2-2c=0\implies c=1$. Thus, $y=x+1$ is an asymptote for $x\to \infty$ case.
Let $x=ky+b$. We will get
$$
2(k^2-2k)y^2 + (4kb +3k -2b-1)y \cdots = 0
$$
Then $2k^2-2k=0\implies k=0$ or $k=1$. Use the second condition $4kb+3k-2b-1=0$ to see that if $k=0$, then $b=-\frac{1}{2}$; if $k=1$, then $b=-1$. Thus, we have two asymptotes for $y\to \infty$ case:
$$
x=-\frac{1}{2}
$$
$$
y=x+1
$$
The graph: