Xiao (Anthony) Hong

Poetry is the art of calling the same thing by different names. – Anonymous.

Yes, and mathematics is the art of calling different things by the same name. – Henri Poincaré.

About Me

Me in front of Olin Library.

Hello! I am Anthony, a senior undergraduate at Washington University in St. Louis, majoring in a joint major Econ+CS, with a double major in Mathematics. I will do my Math PhD at Rice University next fall. My early study in architecture and art led me to an interest in geometry, which I now explore with an additional layer of data in a broad sense. I’m interested in various geometric structures, including Riemannian and symplectic geometry, as well as probabilistic and coarse geometry. I also enjoy visual models like knots, graphs, polytopes, and some low-dimensional manifolds. I like drawing these models either by hand or in vector graphics.

Recently, I finished my undergraduate thesis in symplectic and toric manifolds with Prof. Xiang Tang. Last summer, I participated in an REU on discrete differential geometry and geometry processing at MIT SGI.

Outside of math 🔢, I enjoy reading social theories 📖, listening to classical music 🎻, traveling ⛰️, and spending time with my cat 🐈.

My cat Qiu-qiu.

Contact

Email: hong[dot]x@wustl[dot]edu
LinkedIn: https://www.linkedin.com/in/xiao-hong-anthony/
Twitter: https://x.com/AnthonyHongXiao
Photo: New York. Dec 2022.

Talks/Teaching

Speaker at Midstates Consortium for Math and Science 23 (session I.B.3) at University of Chicago. (beamer presentation). The work was also presented at Prof. Martinkainen’s session and WashU SP24 Undergraduate Research Symposium (video).
My undergraduate thesis presentation (video and event link).
Teaching assistant for Math5046 Differential Topology.
Grader for Math4111 Introduction to Analysis, Math4171 Topology I, and Math5051 Measure Theory and Functional Analysis I.

Seminars/Workshops

Math540 Index Theorem.
Math547 Lie Algebra and Representation Theory.
Aryclic Painting: Urbanity and Space. Aug 2020.
Math560 Compact Lie Groups.
Math586 Network Statistics.
Math547 Combinatorics of Polytopes.
Math497 Group Theory From a Historical Perspective
UNC Undergraduate Analysis and PDE Seminar FL22-SP24.
WashU Reading Group SP23: Algebraic Geometry.
WashU Reading Group FL23: Representation Theory.
StanCon 2023 Workshop: Convention on Stan Programming and Bayesian Modeling
WUSTL Metamorphic Architecture Workshop 2019, mentored by Prof. Heather Woofter and Prof. Sung Ho Kim.

Publications

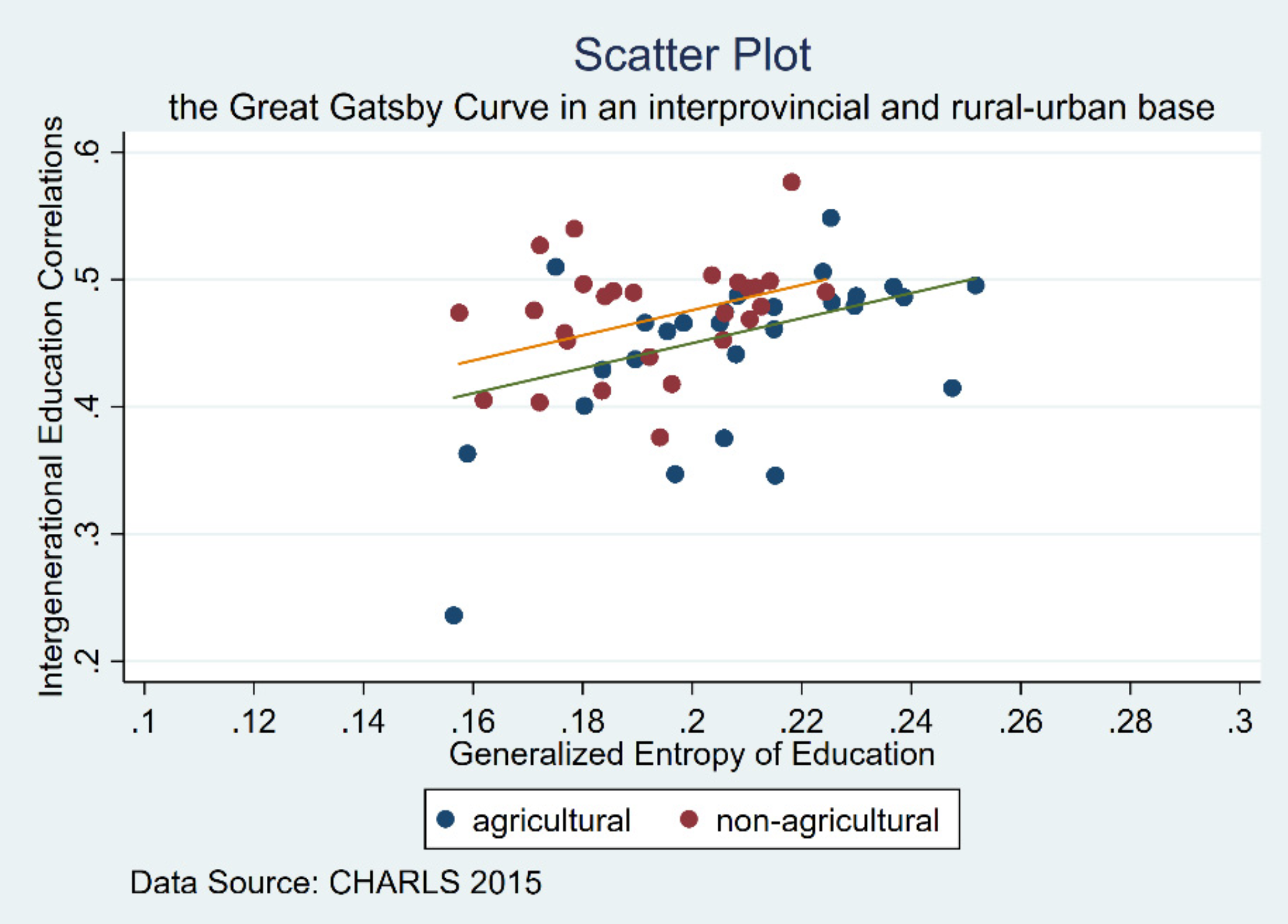The Great Gatsby Curve.

1. Study of Intergenerational Mobility and Urbanization Based on OLS Method and Ordered Probit Model

IEEE-CS/MSIEID2020, Dec 18 2020.

DOI: 10.1109/MSIEID52046.2020.00092

The study based on the CHARLS dataset uses OLS, ordered probit model, and generalized entropy to analyze and generate Great Gatsby curve and Lorenz curve. The study reveals a growing educational disparity across generations in China, highlighting an increasing trend in educational inequality despite overall improvements, especially between urban and rural regions.

Interestingly, besides the educational version of Great Gatsby curve above, there is recently an academic version of Great Gatsby curve.

Projects

1. Undergraduate Thesis on Symplectic Geometry

Feb 2024 - March 2025

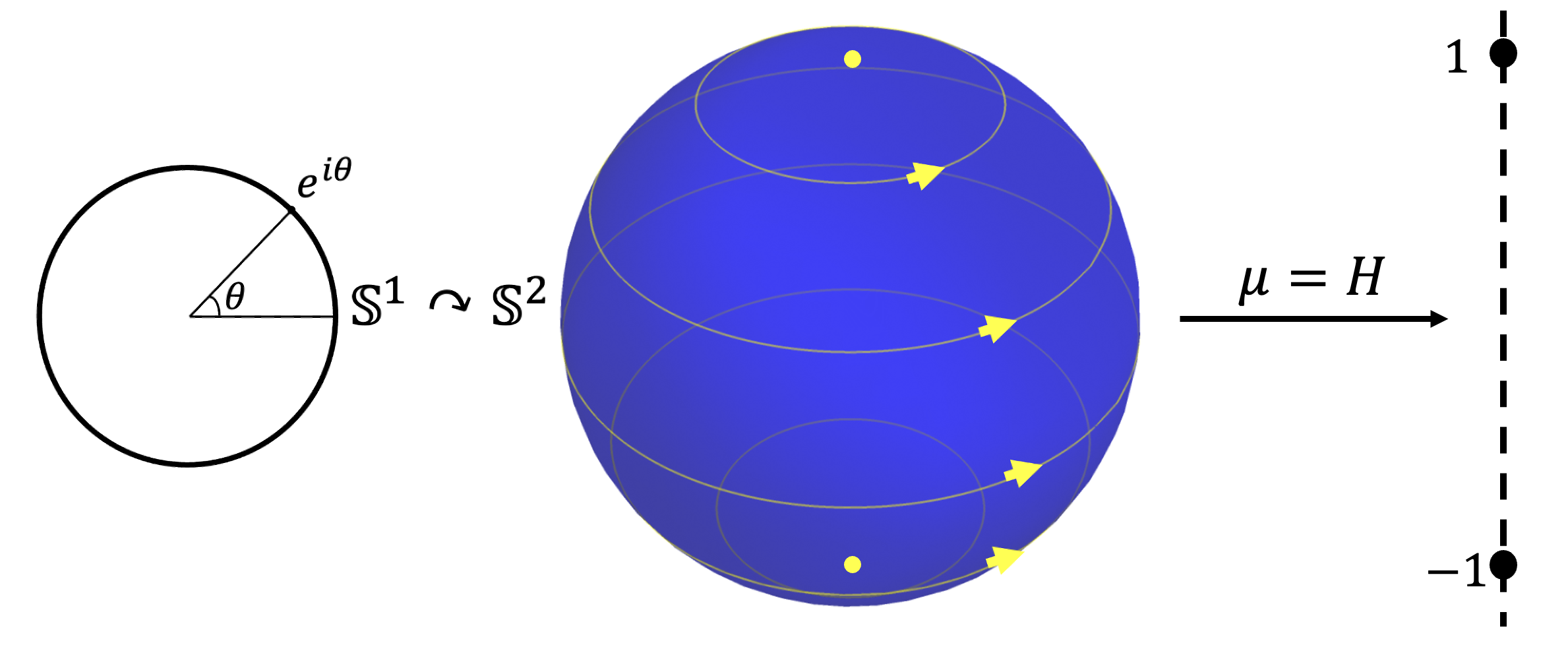Height function as a moment map.

In this thesis, we review the classical results of symplectic geometry, focusing on the Marsden-Weinstein- Meyer Theorem, the Atiyah-Guillemin-Sternberg Theorem, and Delzant’s classification of the symplectic toric manifolds. We begin with preliminaries covering symplectic manifolds, compatible triples, Morse the- ory, Lie groups, and Hamiltonian actions, including examples like circle actions and complex projective space with Fubini-Study form. The thesis concludes with some applications and generalizations of these classical theorems: Horn’s conjecture on Hermitian spectra, Kirwan and Weinstein ’s generalization of the convexity theorem, and the principle of quantization commuting with reduction.

Paper link | Presentation link

2. Curvature of Cayley Graph of Abelian and Nilpotent Groups

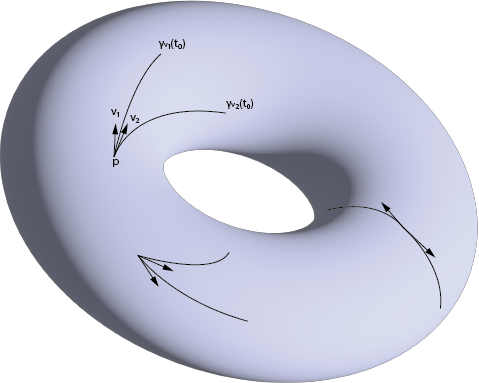Evolving Point Measures.

Jul 2023 - Jan 2024

This is a summer research with Prof. Renato Feres beginning in July 2023. The study aims to use efficient algorithms to compute Ollivier-Ricci curvature, or Lin-Lu-Yau curvature, of Cayley graphs of certain groups and find out some patterns. Currently, efficient optimization algorithm is found for Cayley graph and theoretical justifications for interesting patterns about curvature are concluding.

There is also a second project I am working with Prof. Feres. The project studies the Wasserstein distance of point measures that evolved along their geodesics after initiations.

$$ W_p(\mu_1,\mu_2)=\left(\inf_{\mu\in \Gamma(\mu_1,\mu_2)}{\int_{X^2}d(x,y)^pd\mu(x,y)}\right)^{\frac{1}{p}}=\left(\inf_{\mu\in \Gamma(\mu_1,\mu_2)}{\mathbf{d}(\mu,\nu)^p_{L^p(\mu;X)}}\right)^{\frac{1}{p}} $$ with $$ \forall A\in \mathcal{B}(\mathcal{M}):\text{ }\mu_1(t)(A)=\frac{1}{n}\sum_{i=1}^{n}{\delta_{\gamma_{v_i}(t)}}(A)=\frac{\text{ number of }\gamma_{v_i}(t)\text{ in }A}{n}. $$

MNIST digit examples.

3. Image Classification Using Wasserstein Distance from Monge-Kantorovich Solvers

Final project in Prof. Yixin Chen’s CSE543 Nonlinear Optimization, with Jingyuan Zhu, Mingzhen Li, Ruiqi Wang, Fall 2023.

A review of the paper on gradient descent and finite element method for solving the Monge-Kantorovich problem with quadratic cost $$ \inf_{T\in \Gamma(\mu,\nu)}\left(\int_X \frac{1}{2}\left|x-T(x)\right|^2 d\mu\right)^{1 / 2} $$ with application in image classification.

Paper Link; image from the database.

4. MIT Summer Geometry Initiative (SGI)

Jul 2024 - Aug 2024

The MIT SGI is a program that starts with a week-long tutorial in geometry processing, followed by group projects mentored by experts in the field. Below are the projects I contributed to:

Deforming Mesh (Dr. Nickolas Sharp)

In this project, I explored different metrics to compare the “wiggliness” of shapes, focusing on Gromov-Hausdorff, Hausdorff, and Chamfer distances. The project involved applying these metrics to analyze and quantify shape dissimilarities. My work contributed to developing a deeper understanding of how these distances can be used in practical geometry processing applications.

Project Link

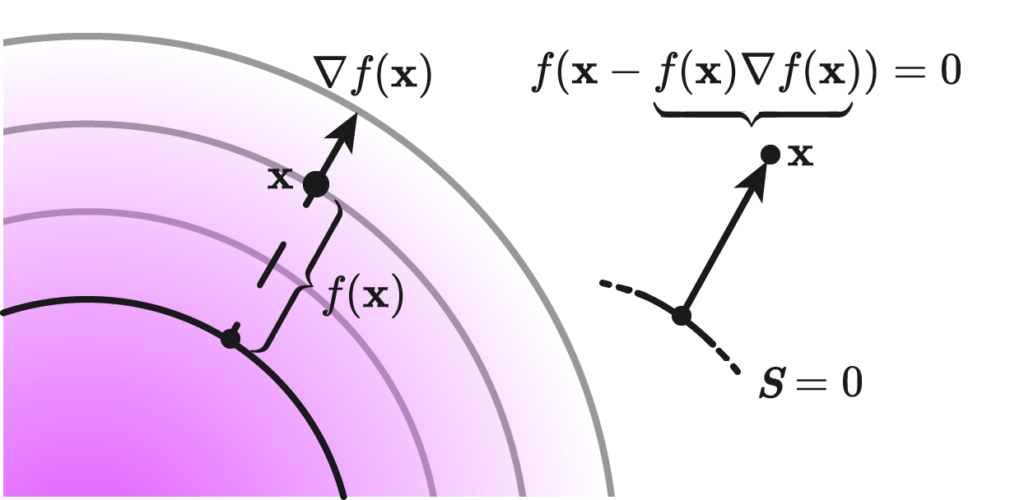
Signed Distance Functions (SDFs) (Prof. Oded Stein and Prof. Silvia Sellán)

This project involved designing and reconstructing signed distance functions (SDFs) using the marching squares algorithm. We studied how SDFs can be characterized on planes, proving a theorem that connects SDFs to the Eikonal equation and the closest point condition. The project aimed at improving the precision of surface reconstructions, which has broad implications for fields like computer graphics and computational geometry.

Part 1 | Part 2

Fitting Inconsistent Input with Noise Regularization (Prof. Amir Vaxman)

In this project, I worked on reconstructing surfaces from point clouds that include noise and outliers. We utilized shallow neural networks coupled with adversarial modules to regularize the noise and improve the surface fitting process. The project demonstrated how combining machine learning with geometric techniques can lead to more robust and accurate surface reconstructions, even with imperfect data.

Project Link

Winding Numbers Vectorization (Prof. Edward Chien)

This project focused on computing winding numbers, which are essential in understanding the topological properties of shapes. I worked on applying these calculations to a torus and its universal cover, using intrinsic triangulations to optimize the mesh. The project aimed at solving issues related to mesh connectivity and color region disconnections by embedding these properties in a feature space. The work has practical implications for texture mapping and mesh processing in computer graphics.

Project Link: coming soon.

Bridging Curvatures: From Riemann to Gauss

This project aimed to introduce the concept of curvature to a broader audience, particularly those familiar with surface curvatures. I reviewed the isometric embedding of a flat torus and explored Gromov’s convex integration technique. The project served as an educational resource, connecting classical differential geometry concepts with more advanced topics, making them accessible to members of the SGI community.

Project Link; image from paper.

5. Hex & Brouwer Paper Report

Hex board game.

Midterm project in Prof. Chi’s Math 4181 Algebraic Topology, Spring 2022.

Report Link

A report that correctsm a error on neighborhood size and reestablishes the proof of equivalence between the Hex theorem and the Bouwer Fixed-Point in David Gale’s paper “The Game of Hex and The Brouwer Fixed-Point Theorem.”

Image from Wolfram.

6. Split Spoils: Solution to Stolen Necklace Problem Via Borsuk-Ulam Theorem

Final project in Prof.Chi’s Math 4181 Algebraic Topology, Spring 2022.

Report Link

Aiming for high-schooler reading, the paper demonstrates how to solve a mathematical problem. Specifically, guided by Using the Borsuk-Ulam Theorem and 3b1b YouTube video on necklace problem, we presented the Borsuk-Ulam Theorem intuitively and used it to solve the 2-dimensional Necklace division problem.

A covering.

7. A Note about Algebraic and Geometric Characteristics of Archetypal Riemann Surfaces

Final project in Dr. Rodsphon’s Math 497 Topic in Group Theory, Spring 2023.

A.B. Sossinsky in Geometries classified subgroups of $\text{SO}(3)$ and $\text{Isom}(\mathbb{R}^2)$ for Platonic bodies and tillings. Aimed for understanding such visual applications, we wrote a summary of curvatures, isometry groups, and automorphism groups of 3 Riemann Surfaces $\hat{\mathbb{C}}, \mathbb{C}, \triangle$ in uniformization theorem. Paper Link

Presentation: An Exposition of Modernism in Geometry and Physics

Gallery

Final critique, Metamorphic Workshop 2019.

Market-Pavilion Continuum (detail), Metamorphic Workshop 2019.

Model: The Memory Museum. Made in 12/2019.